It is still 310 B.C., you are still in Math Club
in Alexandria, Egypt, and your best friend Eratosthenes has so far calculated:
1) The diameter of the Earth (24,000 miles)
2) The circumference of the Moon's Orbit (1,480,000
miles)
3) The Diameter of the Moon (2160 miles)
By now, there is little Erathosthanes could announce that would surprise you. Today, there was a perfect solar eclipse, and Eratosthanes indicated that because the Moon exactly covered the sun during the totality of the eclipse, he could compute the Diameter of the Sun. You have learned to sigh, and listen, since he is rarely wrong.
Here is what Eratosthenes declares you need to know to solve the problem:
1) The moon's diameter is 2160 miles
2) The circumference of the moon's orbit is 1,480,000 miles, or the
distance from the earth to the moon is about 724,000 miles
3) The moon exactly covers the sun during a solar eclipse
4) The distance from the earth to the sun is 92 Million Miles (This
is one of the few things the Greeks had a hard time calculating,
so I'm including it here)
How did Eratosthenes figure this out, and what is the distance from the sun to the earth? (remember we're still on equivalent ratios)
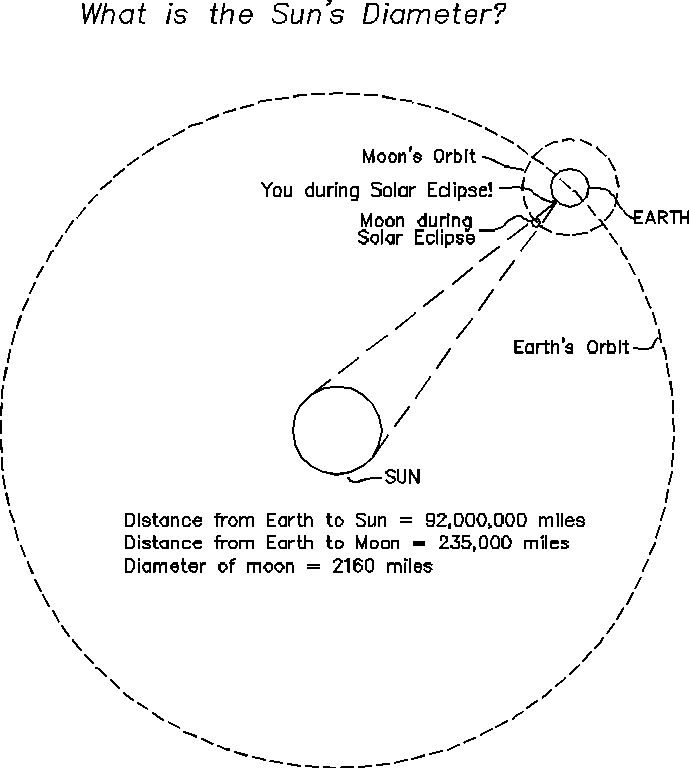
We need to form a ratio of equivalent quantities:
(diameter of sun) / (diameter of moon) = (distance to sun) / (distance to moon)
(diameter of sun) = (diameter of moon) * (distance to sun) / (distance to moon)
Earlier information:
(diameter of moon) = 2160 miles
(distance to moon) = 235,000 miles
(distance to sun) = 92,000,000 miles
Soooo....
(diameter of sun) = (2160 miles) * (92,000,000 miles) / (235,000 miles) = 845,000 miles
Hopefully, you've now mastered these ratios of equivalent quantities!
This is what people did before Pokemon!