It is still 310 B.C., you are still in Math Club
in Alexandria, Egypt, and your best friend Eratosthenes has so far determined
that
1) The earth is 24,000 Miles in circumference (problem
#1)
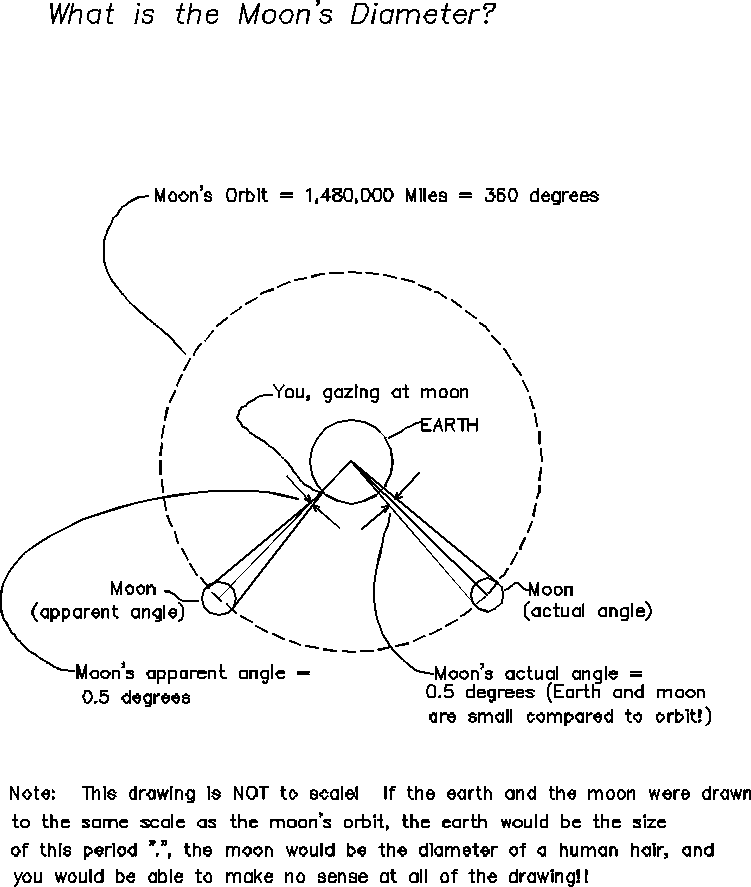
2) The circumference of the moon's orbit around
the Earth is 1,480,000 miles (problem #2).
Now, Eratosthenes announces that he can determine the Diameter of the moon, and therefore, its Circumference.
By now, you have learned not to be surprised by these announcements. Eratosthenes has used an angle measuring device called a protractor, and determined that the moon is 0.5 degrees of arc in the sky.
1) What is the moon's diameter?
2) What is the moon's circumference?

We need to form a ratio of equivalent quantities:
(angle of moon in sky)/(degrees in an entire orbit) = (moon's diameter) / (moon's orbit)
replacing with the given information, we have
(angle of moon in sky) = 0.5 degrees
(degrees in an entire moon's orbit) = 360 degrees
(moon's orbit) = 1,480,000 miles (we solved
for this in problem #2)
(moon's diameter) = (angle of moon in sky) * (moon's orbit) / (degrees in an entire orbit)
(moon's diameter) = (0.5 degrees) * (1,480,000 miles) / (360 degrees) =
(moon's diameter) = 2055 miles!
(moon's circumference) = 3.14 * (moon's diameter) = 6450 miles (like
driving across the US and back)