It is still 310 B.C., you are still in Math Club in Alexandria, Egypt, and your best friend Eratosthenes has used his well and your well to determine that the earth is 24,000 miles in circumference, as we described in problem #1 last week.
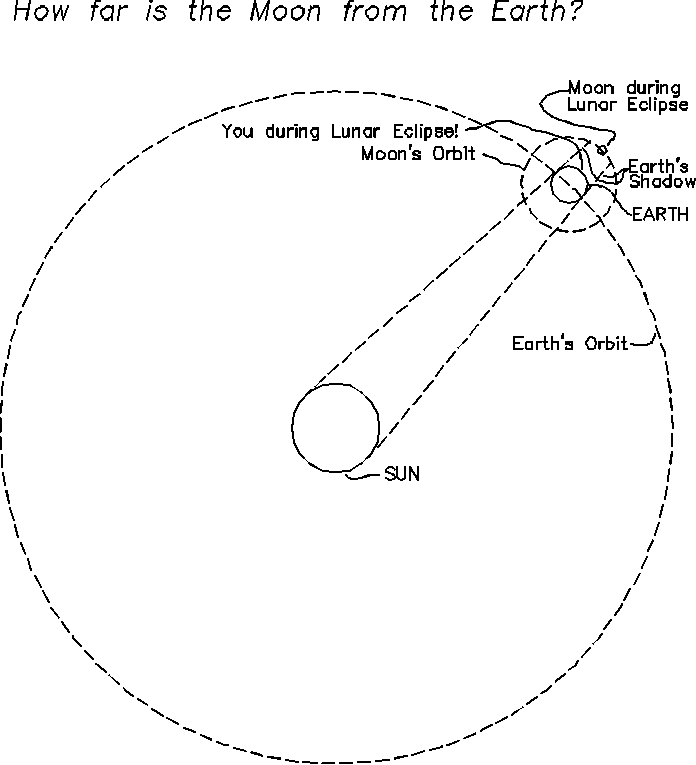
While the two of you are discussing this one evening, you look up and notice that a lunar eclipse (the earth is blocking light from reflecting off the moon) has begun, and that the total eclipse (no illumination of the moon at all) lasts exactly 3 hours 20 minutes. Furthermore, you have observed in the past that during a solar eclipse (the moon travels in front of the sun), that the moon happens to exactly cover the sun, as if you were stacking two pennies on top of each other. (Note: NEVER look at the sun during a solar eclipse!! Cut a pinhole in a piece of foil and look at the shadow the pinhole casts)
When the lunar eclipse is over, Eratosthenes leaps to his feet and announces that since there won't be any cartoons to watch for another 2200 years, he wants to work on calculating the circumference of the moon's orbit around the earth! You are astonished once again. Why, you're still writing on papyrus scrolls, and is will be 1800 years before Galelio peers through a telescope!
Here is what we need to know:
1) The moon's orbit takes 27 days (why is it shorter than 28 from full
moon to full moon?)
2) The eclipse lasted 3 hours 20 minutes
3) From last week, we know the earth's circumference is 24,000 miles
4) The ratio of the circumference of a circle to its diameter is always
3.1 or so
How did Eratosthenes figure this out, and what is the circumference of the moon's orbit? (remember we're still on equivalent ratios)
This is what people did before cartoons!

We need to form a ratio of equivalent quantities:
3 hours 20 min = 3.33 hours
27 days = 648 hours
Earth's shadow = Earth's diameter = Earth's circumference/3.14 = 24,000
miles/3.14 = 7640 miles
We want to know the circumference of the moon's orbit. Think
of this as expressing ratios of similar things in similar ways. For
this case, we divide the length of the orbit during the eclipse (the earth's
shadow) by the entire
orbit, and the equivalent ratio in time is the time the moon is in
eclipse divided by the time for the moon to go the entire orbit:
7640 miles / C = 3.33 hours / 648 hours
C = 7640 miles * 648 hours / 3.33 hours = 1,480,000 miles!