#1 Eratosthenes measures the circumference of the Earth!

Equivalent Ratios of different quantities, part 1

JLS 6th Grade MATH CLUB
Equivalent Ratios of different quantities
1/19/2000
Jay Chesavage (jay_nospam@chesavage.com)

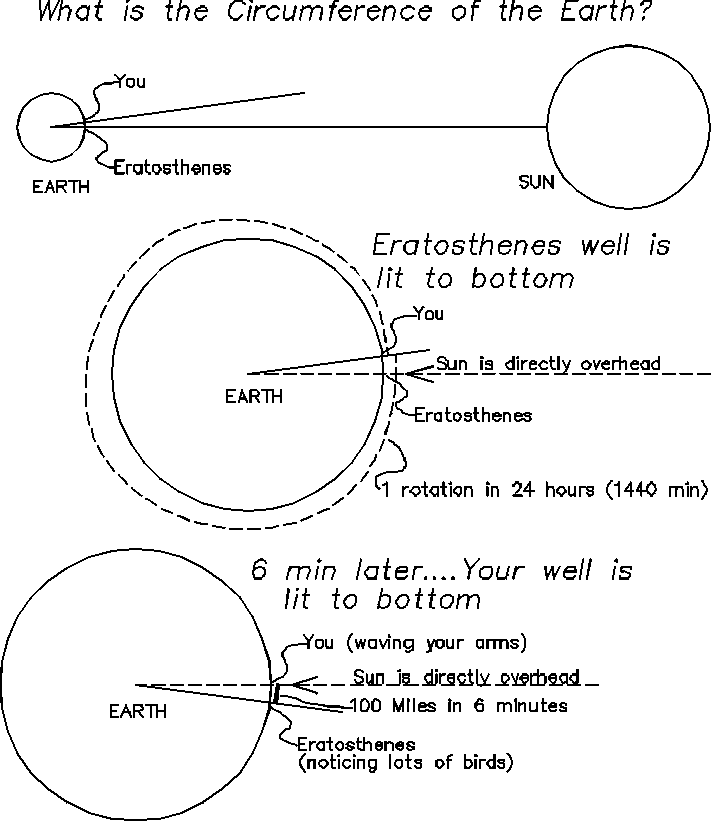
It is now 310 B.C., you are in Math Club in Alexandria, Egypt, and your best friend Eratosthenes has announced that he can figure out the circumference of the earth using only:

The Sun
Two long, deep wells, one in his back yard and one in your uncle's back yard, which is exactly 100 miles WEST of his well.
A minute glass calibrated in minutes.

At around noon, Eratosthenes knows that the sun will exactly light up his deep well shaft all the way to the bottom. You are to sit by your well in your uncle's back yard, and wave your arms madly when your well is illuminated all the way to the bottom. This will quickly frighten the thousands of crows that gather in your uncle's back yard (your Aunt likes to feed crows, and thousands of them gather each day), and they will instantly fly into the air, alerting Erathosthenes that the sun is now directly over your well. Erathosthenes starts the minute glass as soon as his well is illuminated all the way to the bottom, and exactly 6 minutes later notices a thick cloud of crows to the west.

1) So what is the earth's circumference?
2) O.K. there really weren't any crows around, but there were two wells separated by 500 miles. What really happened in 310 B.C. is that Eratosthenes went to the second well on the very day (summer solstice) he knew the first well was illuminated, and measured that the second well was illuminated 7.5 degrees off vertical (there are 360 degrees in a circle). What is the earth's circumference using this measurement?

Solution:

1) The earth's circumference can be determined by equivalent ratios of distance and time:
(diameter of the earth) / (distance between wells) = (minutes in a day) / (minutes between wells fully illuminated)

diameter of the earth = distance between wells * (minutes per day) / (minutes between wells fully illuminated)
diameter of the earth = 1440 * 100 miles / 6 minutes = 24,000 Miles

2) Another equivalent ratio expressed above using equivalent ratios of distance and angular degrees:
(diameter of the earth) / (360 degrees for 1 rotation) = (distance between wells) / (angular difference seen at second well)
diameter of the earth = 360 degrees * (distance between wells) / (angular difference) = 360 * 500 miles / 7.5 degrees = 24,000 miles