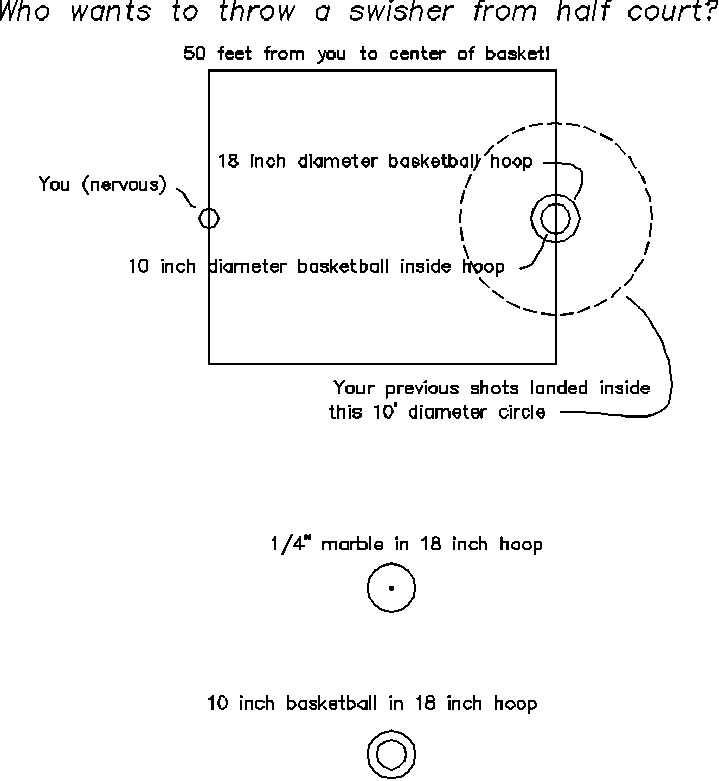
You were given free tickets to go see the Warriors Basketball team play,
and at half time, there is always a contest where they have some kid come
out try to throw a swisher from the half-court line. This time, it
is YOU! Your number was called, and now you are nervously standing
at half court, as shown in the drawing below. You are handed a basketball,
and note that the contest says "throw a swisher", but doesn't say what
you should use to throw your swisher with.
You are nervous because all the television cameras
are pointed at you. In your nervousness, you notice that you have
a marble in your pocket. You begin to wonder whether it would be
any easier if you threw a marble instead of the basketball. You know
that you're not a great shot, and on every attempt you've every made, your
ball has landed within 5 feet of the basket (a 10 foot diameter circle)
Here are some important facts:
1) The formula for the area of a circle is (diameter) * (diameter)
* 3.14 / 4, or some of you may have heard it described as 3.14 * (radius)
* (radius), which is the same as the formula above.
2) The basketball has a 10 inch diameter
3) The hoop has an 18 inch diameter
4) The marble has a 1/4 inch diameter (small marble)
5) You are a bad shot, and have an equal probability of landing anywhere
in the 10 foot diameter circle, but never throw outside this circle.
1) What would the probability of getting a "swisher" - a shot through the basket where the ball doesn't touch the sides, if you used the marble?
2) What would the probability of getting a "swisher" if you used the basketball?

Let's imagine that the hoop was half of the area of the 10 foot diameter circle. This is to say that 1/2 the area is inside the circle, and 1/2 the area is outside the circle. What would the probability of landing inside the circle be? 1/2, right?
OK, so shooting into a 7 foot diameter hoop (this is the size which contains 50% of the area of a 10 foot diameter circle) would look kind of silly, it gives us an idea of how to approach the problem. The probability of shooting something small into the hoop is equal to:
(the area that makes the swisher) / (the total area)
The total area in our 10 foot diameter circle = (120 inch) * (120
inch) * 3.14 / 4 = 11,304 square inches
Now the area inside the hoop is an interesting question. If we put very small object, such as a marble inside the hoop, we can use the entire area of the 18 inch diameter hoop, which is
(area that makes a swisher) = (area in 18 inch diameter hoop) = (18 inch) * (18 inch) * 3.14 / 4 = 254 square inches.
So, the likelihood of getting a shot with the marble is 254 square inches
/ 11,304 square inches = .02, or about
1 out of 50 to get a basket using the marble.
Throwing a basketball is an interesting case. Take a look at the bottom drawing in the above figure. If you throw a 10 inch basketball into an 18 inch hoop, you have to keep the basketball away from the sides of the hoop. With a marble, you can throw all the way up to the side of the hoop without worrying about bouncing off the rim. With the 10 inch basketball in the 18 inch rim, you have to throw the ball inside an 8 inch diameter circle in the middle of the rim, or you'll hit the rim and miss (sketch this out for yourself and see!). If the basketball were just 1 inch smaller than the rim, you would have to hit a 1 inch circle to swish!.
For the case of throwing the 10 inch basketball in an 18 inch rim, we have
(area that makes a swisher) = (area in 8 inch diameter swisher zone) = (8 inch) * (8 inch) * 3.14 / 4 = 50 square inches.
So, the likelihood of getting a shot with the basketball is 50 square
inches / 11,304 square inches = .004, or about
1 out of 250 to get a basket using the basketball.
So your chances are 5 times better using the marble than the basketball!